the personal blog with Hexo, theme Fan. Record every bit of learning and life.

多年来，随着对 Web 应用程序的需求增多，Web 浏览器的功能也不断增强。从而，可以找到实现类似功能的多种方法。本文将介绍一类很少被人关注的功能：在浏览器选项卡之间进行通信。以下是列举的几个适用场景：

• 将对应用程序的主题修改（例如，深色或浅色主题）应用到所有已打开的浏览器选项卡中。
• 请求用于身份验证的最新令牌，并在浏览器选项卡之间共享。
• 跨浏览器选项卡同步应用程序状态。

本文主要介绍几种跨浏览器通信的方法。然而，每种方法都有其优缺点。因此，本文会详细讨论它们，以便让您能够在实际开发中找到适用的最佳方法。

1. 使用本地存储事件 LocalStorage

通过使用 LocalStorage，可以使得同一应用程序源中的选项卡之间进行通信。同时 LocalStorage 也支持事件，可以使用此功能跨浏览器选项卡进行通信，存储更新后，其他选项卡将接收事件。

例如，在一个选项卡中执行以下 JavaScript 代码。

1

window.localStorage.setItem("theme", "dark");

如下所示，监听事件的其他选项卡将接收它：

1
2
3
4
5
6

window.addEventListener('storage', (event) => {
    if (event.storageArea != localStorage) return;
    if (event.key === 'theme') {
        // 测试使用 event.newValue
    }
});

codesandbox demo

2. 使用 BroadcastChannel API 接口

BroadcastChannel API 允许选项卡、窗口、Frames、Iframes 和 Web Workers 之间的通信。一个选项卡可以创建一个 Channel 并在其中发送消息，如下所示：

1
2

const channel = new BroadcastChannel('app-data');
channel.postMessage('post');

其他选项卡可以监听频道，如下所示：

1
2
3
4
5
6
7
8
9

const channel = new BroadcastChannel('app-data');

channel.addEventListener ('message', (event) => {
    console.log(event.data);
});

// Disconnect the channel
channel.close();

codesandbox demo

这样，浏览器上下文（Windows、Tabs、Frames、或 Iframes）之间可以进行通信。尽管这是浏览器选项卡之间的一种很便捷的通信方式，但 safari 和 IE 是不支持这种方式的。可以在 MDN 的 BroadcastChannel 文档中查看详细信息。

3. 使用 Service Worker 发送消息

可能会有疑问，Service Worker 是如何进入这种场景的。不过从根本上来说，Service Worker 支持发送消息，可以使用这些消息在浏览器选项卡之间进行通信。
使用 Service Worker，可以发送如下所示的消息：

1
2
3

navigator.serviceWorker.controller.postMessage({
    broadcast: data
});

同时在接收 Worker 的其他浏览器选项卡中可以监听事件。

1
2
3
4
5
6
7
8

addEventListener('message', async (event) => {
    if ('boadcast' in event.data ) {
        const allClients = await clients.matchAll();
        for (const client of allClients) {
            client.postMessage(event.broadcast);
        }
    }
});

这种方法提供更多的控制保障，是传递消息的可靠方法。但是，实现 Service Worker 需要一些关于 Service Worker API 的补充知识和额外工作。所以，在这种情况下，如果其他方法都不起作用，最好还是尝试这个方法。可以在 MDN 的 Service Worker API 文档中找到更多信息，还有一个完整的示例。

4. 使用 Service Worker 发送消息

Window.postMessage() 方法是跨浏览器选项卡、弹出窗口和 Iframes 进行通信的传统方法之一。可以按如下方式发送消息.
Syntax
targetWindow.postMessage(message, targetOrigin, [transfer]);

1
2

const targetWindow = window.opener;
targetWindow.postMessage(message, targetOrigin)

目标窗口可以监听事件，如下所示：

1
2
3
4

window.addEventListener("message", (event) => {
    if (event.origin !== "http://localhost:8080") return;
    // 可以做测试
}, false);

与其他方法相比，这种方法有一个优点：可以支持跨源通信。但它也有一个限制：需要引用另一个浏览器选项卡。所以这种方法只适用于通过 window.open() 或 document.open() 方法。可以在 MDN 文档中找到更多信息。

codesandbox demo

mac/ubuntu/linux 配置sudo免密码

1
2
3
4
5
6

1 打开命令窗口输入如下命令：
sudo visudo 或者  sudo vi /etc/sudoers
2 替换 #%admin ALL=(ALL) ALL 为
%admin ALL=(ALL) NOPASSWD: NOPASSWD: ALL

在撰写本文时，以下新的JavaScript提案功能已进入第4阶段，并且几乎肯定会包含在ES2021中。您已经可以开始在最新版本的浏览器，Node.js和Babel中使用。

注意：ECMAScript是JavaScript所基于的标准，由TC39委员会管理。ECMAScript始终是一个不需要的名称，这会使所有内容对初学者都感到困惑。人们经常谈论JavaScript功能，但参考的是ECMAScript规范。

Numeric Separators

1
2
3
4
5
6

1_000_000_000 // decimal literals
0b1010_0001 // binary literals
101_475_938.38 // floating-point literals
0.000_001 // in fractional part
1e10_000 // in exponent part

Logical Assignment

支持与新的运营逻辑分配 &&=，||= 和 ??=。与它们的 mathematical and bitwise counterparts不同，逻辑分配遵循其各自逻辑操作的短路行为。仅当逻辑运算将评估右侧时，它们才执行分配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

// falsy: false, 0, -0, 0n, "", null, undefined, and NaN
// truthy: all values are truthy unless defined as falsy
// nullish: null or undefined

a ||= b
// Logical OR assignment
// Equivalent to: a || (a = b);
// Only assigns if a is falsy

a &&= b
// Logical AND assignment
// Equivalent to: a && (a = b);
// Only assigns if a is truthy

a ??= b
// Logical nullish assignment
// Equivalent to: a ?? (a = b);
// Only assigns if a is nullish

// examples: 

// Logical Assignment Operator with && operator
let a = 1
const b = 2
a &&= b
console.log(a) // 2
// Equivalent to
// 1. a && (a = b)
// 2. if (a) a = b

// Logical Assignment Operator with || operator
let a
const b = 2
a ||= b
console.log(a) // 2
// Equivalent to
// 1. a || (a = b)
// 2. if (!a) a = b

// Logical Assignment Operator with ?? operator
let a
const b = 2
a ??= b
console.log(a) // 2
a = false
a ??= b
console.log(a) // false
// Equivalent to
// a ?? (a = b)

Weak references and finalizers

此功能包含两个高级对象WeakRef和FinalizationRegistry。根据使用情况，这些接口可以单独使用，也可以一起使用。正确使用它们需要仔细考虑，如果可能，最好避免使用它们。

WeakRef 是一个更高级的 API，它提供了真正的弱引用，Weakref 实例具有一个方法 deref，该方法返回被引用的原始对象，如果原始对象已被收集，则返回 undefined 对象。

1
2
3
4
5
6

// Create a WeakRef object referring to a given target object
const ref = new WeakRef(targetObject)

// Return the WeakRef instance's target object, or undefined if the target object has been garbage-collected
const obj = ref.deref()

使用FinalizationRegistry对象可以在垃圾回收对象时请求回调。

1
2
3
4
5
6
7
8
9

// Create a registry object that uses the given callback
const registry = new FinalizationRegistry([callback])

// Register an object with a registry instance so that if the object is garbage-collected, the registry's callback may get called
registry.register(target, heldValue, [unregisterToken])

// Unregister a target object from a registry instance
registry.unregister(unregisterToken)

Promise.any()

Promise.any 方法和 Promise.race 类似——只要给定的迭代中的一个 promise 成功，就采用第一个 promise 的值作为它的返回值，但与 Promise.race 的不同之处在于——它会等到所有 promise 都失败之后，才返回失败的值：

1
2
3
4
5
6
7
8
9
10

Promise.any(promises).then(
    (first) => {
        // Any of the promises was fulfilled.
    },
    (error) => {
        // All of the promises were rejected.
        // error instanceof AggregateError
    }
)

String.prototype.replaceAll

当前，如果不使用全局正则表达式，就无法替换字符串中子字符串的所有实例。与字符串参数一起使用时，String.prototype.replace仅影响首次出现。

String.prototype.replaceAll() 将为开发人员提供一种简单的方法来完成此常见的基本操作。

1
2
3

'139****1234'.replaceAll('*', 'x') // '139xxxx1234'
'abcabc'.replaceAll(/b/g, 'A') // 'aAcaAc'

参考文章

数字分隔符
逻辑分配
Weak references and finalizers
Promose.any()
String.prototype.replaceAll()

CSS3实现右侧箭头(烦躁、画个箭头消消火)

1
2

<div class='right-arrow' /> 

• 实现方式一

  1 2 3 4 5 6 7 8

  <!-- 实现方式一 --> width: 8px; height: 8px; border-bottom: 2px solid rgba(255, 255, 255, 0.7); border-right: 2px solid rgba(255, 255, 255, 0.7); transform: matrix(0.71, -0.7, 0.71, 0.71, 0, 0);

• 实现方式二

  1 2 3 4 5 6 7

  <!-- 实现方式二 --> width: 8px; height: 8px; border-bottom: 2px solid rgba(255, 255, 255, 0.7); border-right: 2px solid rgba(255, 255, 255, 0.7); transform: rotate(45deg);

• 实现方式三(SVG)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

<svg width="750" height="500">
  <polyline points="
    3 3
    30 28
    3 53
  "></polyline>
</svg>

 svg {
      stroke: #000;
      stroke-width: 2;
      stroke-linecap: round;
      stroke-linejoin: round;
      fill: none;
    }

• 实现方式四(Canvas)

1
2
3
4
5
6
7
8
9
10
11

<canvas id="canvas" width="500" height="400">您的浏览器不支持canvas</canvas>
<script>
    const canvas = document.getElementById("canvas");
    const ctx = canvas.getContext("2d");
    ctx.moveTo(0, 0); // 开始坐标在 (0, 0)
    ctx.lineTo(10, 10); // 线条移动到 (10, 10)
    ctx.lineTo(0, 20); // 线条移动到 (0, 20)
    ctx.strokeStyle = "grey"; // 线条颜色设置为灰色
    ctx.stroke(); // 绘制
</script>

记解决远程仓库文件大小

在React我们习惯把组件文件首字母定为大写，但是今天发现有同事弄了一个骚操作

大概是这个样子

• 新建一个 setting.ts 文件(大小写不敏感的状态下)，并提交
• 修改本地 setting.ts 变为 Setting.ts，文件内容无变更，无法提交
• 执行git config core.ignorecase false，修改 大小写敏感 规则，然后提交，查看结果，此时会存在 大小写 同时存在的文件
• 此时某种机缘下，再次执行 git config core.ignorecase true，大小写不敏感，
• 此时执行 git push ， 即把最新的更新都更新到了 a.ts 中
• 此时再修改 大小写敏感规则为敏感， 执行 git pull ，并不会拿到最新的更新。比如自己想要的是第一次修改后的 Setting.ts ，但是服务器有一个没有更新的 Setting.ts 和 有更新的 setting.ts,而你只能拿到前者，这可能就会出现一些问题

解决办法

执行git config –global core.ignorecase false，全局设置 大小写敏感 。

1. 文件变更比较少的情况

   直接使用以下命令重命名文件，在 git 中不要直接修改文件名，最好的办法是使用下面的方式，

   1 2 3 4 5 6 7 8

   git mv -f [你想要删掉的文件] [你想要留下的文件] git mv -f setting.ts Setting.ts 等同于： git rm setting.ts git add Setting.ts

   这个命令的目的就是删除不需要的大小写同名文件，修改后 git push 提交变更即可。

   或

   1 2	git rm --cached src/.../setting -r

2. 变更比较多时

   • 删除远程分支
   • 本地执行 git rm -r –cached .
   • 然后重新 git push

   mac windows 在不设置大小写敏感规则的时候默认大小写是不敏感，项目部署的机器是 Linux 的，而 Linux 是大小写敏感的。所以这样的问题平时不易发现，本地调试的时候大部分时候并不会出错误，只有在项目部署的时候问题才会显示出来

(转载) 前端工程师的自我修养：React Fiber 是如何实现更新过程可控的

原文地址: https://juejin.cn/post/6911681589558640654?utm_source=gold_browser_extension

前言
从 React 16 开始，React 采用了 Fiber 机制替代了原先基于原生执行栈递归遍历 VDOM 的方案，提高了页面渲染性能和用户体验。乍一听 Fiber 好像挺神秘，在原生执行栈都还没搞懂的情况下，又整出个 Fiber，还能不能愉快的写代码了。别慌，老铁！下面就来唠唠关于 Fiber 那点事儿。

什么是 Fiber

Fiber 的英文含义是“纤维”，它是比线程（Thread）更细的线，比线程（Thread）控制得更精密的执行模型。在广义计算机科学概念中，Fiber 又是一种协作的（Cooperative）编程模型，帮助开发者用一种【既模块化又协作化】的方式来编排代码。

简单点说，Fiber 就是 React 16 实现的一套新的更新机制，让 React 的更新过程变得可控，避免了之前一竿子递归到底影响性能的做法。

关于 Fiber 你需要知道的基础知识

1.浏览器刷新率（帧）
页面的内容都是一帧一帧绘制出来的，浏览器刷新率代表浏览器一秒绘制多少帧。目前浏览器大多是 60Hz（60帧/s），每一帧耗时也就是在 16ms 左右。原则上说 1s 内绘制的帧数也多，画面表现就也细腻。那么在这一帧的（16ms） 过程中浏览器又干了啥呢？

通过上面这张图可以清楚的知道，浏览器一帧会经过下面这几个过程：

• 接受输入事件
• 执行事件回调
• 开始一帧
• 执行 RAF (RequestAnimationFrame)
• 页面布局，样式计算
• 渲染
• 执行 RIC (RequestIdelCallback)

第七步的 RIC 事件不是每一帧结束都会执行，只有在一帧的 16ms 中做完了前面 6 件事儿且还有剩余时间，才会执行。这里提一下，如果一帧执行结束后还有时间执行 RIC 事件，那么下一帧需要在事件执行结束才能继续渲染，所以 RIC 执行不要超过 30ms，如果长时间不将控制权交还给浏览器，会影响下一帧的渲染，导致页面出现卡顿和事件响应不及时。
2. JS 原生执行栈
React Fiber 出现之前，React 通过原生执行栈递归遍历 VDOM。当浏览器引擎第一次遇到 JS 代码时，会产生一个全局执行上下文并将其压入执行栈，接下来每遇到一个函数调用，又会往栈中压入一个新的上下文。比如：

1
2
3
4
5
6
7
8
9
10

function A(){
    B();
    C();
}

function B(){}
function C(){}

A();

引擎在执行的时候，会形成如下这样的执行栈:

浏览器引擎会从执行栈的顶端开始执行，执行完毕就弹出当前执行上下文，开始执行下一个函数，直到执行栈被清空才会停止。然后将执行权交还给浏览器。由于 React 将页面视图视作一个个函数执行的结果。每一个页面往往由多个视图组成，这就意味着多个函数的调用。
如果一个页面足够复杂，形成的函数调用栈就会很深。每一次更新，执行栈需要一次性执行完成，中途不能干其他的事儿，只能”一心一意”。结合前面提到的浏览器刷新率，JS 一直执行，浏览器得不到控制权，就不能及时开始下一帧的绘制。如果这个时间超过 16ms，当页面有动画效果需求时，动画因为浏览器不能及时绘制下一帧，这时动画就会出现卡顿。不仅如此，因为事件响应代码是在每一帧开始的时候执行，如果不能及时绘制下一帧，事件响应也会延迟。
3. 时间分片（Time Slicing）
时间分片指的是一种将多个粒度小的任务放入一个时间切片（一帧）中执行的一种方案，在 React Fiber 中就是将多个任务放在了一个时间片中去执行。
4. 链表
在 React Fiber 中用链表遍历的方式替代了 React 16 之前的栈递归方案。在 React 16 中使用了大量的链表。例如：

使用多向链表的形式替代了原来的树结构

例如下面这个组件：

1
2
3
4
5
6
7
8
9
10
11

<div id="id">
    A1
    <div id="B1">
        B1
        <div id="C1"></div>
    </div>
    <div id="B2">
        B2
    </div>
</div>

• 会使用下面这样的链表表示：
  

• 副作用单链表

• 状态更新单链表

…

链表是一种简单高效的数据结构，它在当前节点中保存着指向下一个节点的指针，就好像火车一样一节连着一节

-遍历的时候，通过操作指针找到下一个元素。但是操作指针时（调整顺序和指向）一定要小心。
链表相比顺序结构数据格式的好处就是：

• 操作更高效，比如顺序调整、删除，只需要改变节点的指针指向就好了。
• 不仅可以根据当前节点找到下一个节点，在多向链表中，还可以找到他的父节点或者兄弟节点。

但链表也不是完美的，缺点就是：

• 比顺序结构数据更占用空间，因为每个节点对象还保存有指向下一个对象的指针。
• 不能自由读取，必须找到他的上一个节点。

React 用空间换时间，更高效的操作可以方便根据优先级进行操作。同时可以根据当前节点找到其他节点，在下面提到的挂起和恢复过程中起到了关键作用。

React Fiber 是如何实现更新过程可控？

前面讲完基本知识，现在正式开始介绍今天的主角 Fiber，看看 React Fiber 是如何实现对更新过程的管控。

更新过程的可控主要体现在下面几个方面:

• 任务拆分
• 任务挂起、恢复、终止
• 任务具备优先级

1. 任务拆分
   前面提到，React Fiber 之前是基于原生执行栈，每一次更新操作会一直占用主线程，直到更新完成。这可能会导致事件响应延迟，动画卡顿等现象。
   在 React Fiber 机制中，它采用”化整为零”的战术，将调和阶段（Reconciler）递归遍历 VDOM 这个大任务分成若干小任务，每个任务只负责一个节点的处理。例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

import React from "react";
import ReactDom from "react-dom"
const jsx = (
    <div id="A1">
            A1
        <div id="B1">
            B1
            <div id="C1">C1</div>
            <div id="C2">C2</div>
        </div>
        <div id="B2">B2</div>
    </div>
)
ReactDom.render(jsx,document.getElementById("root"))

这个组件在渲染的时候会被分成八个小任务，每个任务用来分别处理 A1(div)、A1(text)、B1(div)、B1(text)、C1(div)、C1(text)、C2(div)、C2(text)、B2(div)、B2(text)。再通过时间分片，在一个时间片中执行一个或者多个任务。这里提一下，所有的小任务并不是一次性被切分完成，而是处理当前任务的时候生成下一个任务，如果没有下一个任务生成了，就代表本次渲染的 Diff 操作完成。

挂起、恢复、终止

再说挂起、恢复、终止之前，不得不提两棵 Fiber 树，workInProgress tree 和 currentFiber tree。
workInProgress 代表当前正在执行更新的 Fiber 树。在 render 或者 setState 后，会构建一颗 Fiber 树，也就是 workInProgress tree，这棵树在构建每一个节点的时候会收集当前节点的副作用，整棵树构建完成后，会形成一条完整的副作用链。
currentFiber 表示上次渲染构建的 Fiber 树。在每一次更新完成后 workInProgress 会赋值给 currentFiber。在新一轮更新时 workInProgress tree 再重新构建，新 workInProgress 的节点通过 alternate 属性和 currentFiber 的节点建立联系。
在新 workInProgress tree 的创建过程中，会同 currentFiber 的对应节点进行 Diff 比较，收集副作用。同时也会复用和 currentFiber 对应的节点对象，减少新创建对象带来的开销。也就是说无论是创建还是更新，挂起、恢复以及终止操作都是发生在 workInProgress tree 创建过程中。workInProgress tree 构建过程其实就是循环的执行任务和创建下一个任务，大致过程如下:

当没有下一个任务需要执行的时候，workInProgress tree 构建完成，开始进入提交阶段，完成真实 DOM 更新。
在构建 workInProgressFiber tree 过程中可以通过挂起、恢复和终止任务，实现对更新过程的管控。下面简化了一下源码，大致实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

let nextUnitWork = null;//下一个执行单元
//开始调度
function scheduler(task){
    nextUnitWork = task;
}
//循环执行工作
function workLoop(deadline){
    let shouldYield = false;//是否要让出时间片交出控制权
    while(nextUnitWork && !shouldYield){
        nextUnitWork = performUnitWork(nextUnitWork)
        shouldYield = deadline.timeRemaining()<1 // 没有时间了，检出控制权给浏览器
    }
    if(!nextUnitWork) {
        console.log("所有任务完成")
        //commitRoot() //提交更新视图
    }
    // 如果还有任务，但是交出控制权后,请求下次调度
    requestIdleCallback(workLoop,{timeout:5000}) 
}
/*
* 处理一个小任务，其实就是一个 Fiber 节点，如果还有任务就返回下一个需要处理的任务，没有就代表整个
*/
function performUnitWork(currentFiber){
    ....
    return FiberNode
}

• 挂起

当第一个小任务完成后，先判断这一帧是否还有空闲时间，没有就挂起下一个任务的执行，记住当前挂起的节点，让出控制权给浏览器执行更高优先级的任务。

• 恢复
  在浏览器渲染完一帧后，判断当前帧是否有剩余时间，如果有就恢复执行之前挂起的任务。如果没有任务需要处理，代表调和阶段完成，可以开始进入渲染阶段。这样完美的解决了调和过程一直占用主线程的问题。
  那么问题来了他是如何判断一帧是否有空闲时间的呢？答案就是我们前面提到的 RIC (RequestIdleCallback) 浏览器原生 API，React 源码中为了兼容低版本的浏览器，对该方法进行了 Polyfill。
  当恢复执行的时候又是如何知道下一个任务是什么呢？答案在前面提到的链表。在 React Fiber 中每个任务其实就是在处理一个 FiberNode 对象，然后又生成下一个任务需要处理的 FiberNode。顺便提一嘴，这里提到的FiberNode 是一种数据格式，下面是它没有开美颜的样子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class FiberNode {
    constructor(tag, pendingProps, key, mode) {
        // 实例属性
        this.tag = tag; // 标记不同组件类型，如函数组件、类组件、文本、原生组件...
        this.key = key; // react 元素上的 key 就是 jsx 上写的那个 key ，也就是最终 ReactElement 上的
        this.elementType = null; // createElement的第一个参数，ReactElement 上的 type
        this.type = null; // 表示fiber的真实类型 ，elementType 基本一样，在使用了懒加载之类的功能时可能会不一样
        this.stateNode = null; // 实例对象，比如 class 组件 new 完后就挂载在这个属性上面，如果是RootFiber，那么它上面挂的是 FiberRoot,如果是原生节点就是 dom 对象
        // fiber
        this.return = null; // 父节点，指向上一个 fiber
        this.child = null; // 子节点，指向自身下面的第一个 fiber
        this.sibling = null; // 兄弟组件, 指向一个兄弟节点
        this.index = 0; //  一般如果没有兄弟节点的话是0 当某个父节点下的子节点是数组类型的时候会给每个子节点一个 index，index 和 key 要一起做 diff
        this.ref = null; // reactElement 上的 ref 属性
        this.pendingProps = pendingProps; // 新的 props
        this.memoizedProps = null; // 旧的 props
        this.updateQueue = null; // fiber 上的更新队列执行一次 setState 就会往这个属性上挂一个新的更新, 每条更新最终会形成一个链表结构，最后做批量更新
        this.memoizedState = null; // 对应  memoizedProps，上次渲染的 state，相当于当前的 state，理解成 prev 和 next 的关系
        this.mode = mode; // 表示当前组件下的子组件的渲染方式
        // effects
        this.effectTag = NoEffect; // 表示当前 fiber 要进行何种更新
        this.nextEffect = null; // 指向下个需要更新的fiber
        this.firstEffect = null; // 指向所有子节点里，需要更新的 fiber 里的第一个
        this.lastEffect = null; // 指向所有子节点中需要更新的 fiber 的最后一个
        this.expirationTime = NoWork; // 过期时间，代表任务在未来的哪个时间点应该被完成
        this.childExpirationTime = NoWork; // child 过期时间
        this.alternate = null; // current 树和 WorkInProgress 树之间的相互引用
    }
}

额…看着好像有点上头，这是开了美颜的样子：

是不是好看多了？在每次循环的时候，找到下一个执行需要处理的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function performUnitWork(currentFiber){
//beginWork(currentFiber) //找到儿子，并通过链表的方式挂到currentFiber上，每一偶儿子就找后面那个兄弟
    //有儿子就返回儿子
    if(currentFiber.child){
        return currentFiber.child;
    } 

    //如果没有儿子，则找弟弟
    while(currentFiber){//一直往上找
        //completeUnitWork(currentFiber);//将自己的副作用挂到父节点去
        if(currentFiber.sibling){
        return currentFiber.sibling
        }
        currentFiber = currentFiber.return;
    }
}

在一次任务结束后返回该处理节点的子节点或兄弟节点或父节点。只要有节点返回，说明还有下一个任务，下一个任务的处理对象就是返回的节点。通过一个全局变量记住当前任务节点，当浏览器再次空闲的时候，通过这个全局变量，找到它的下一个任务需要处理的节点恢复执行。就这样一直循环下去，直到没有需要处理的节点返回，代表所有任务执行完成。最后大家手拉手，就形成了一颗 Fiber 树。

• 终止
  其实并不是每次更新都会走到提交阶段。当在调和过程中触发了新的更新，在执行下一个任务的时候，判断是否有优先级更高的执行任务，如果有就终止原来将要执行的任务，开始新的 workInProgressFiber 树构建过程，开始新的更新流程。这样可以避免重复更新操作。这也是在 React 16 以后生命周期函数 componentWillMount 有可能会执行多次的原因。

1. 任务具备优先级
   React Fiber 除了通过挂起，恢复和终止来控制更新外，还给每个任务分配了优先级。具体点就是在创建或者更新 FiberNode 的时候，通过算法给每个任务分配一个到期时间（expirationTime）。在每个任务执行的时候除了判断剩余时间，如果当前处理节点已经过期，那么无论现在是否有空闲时间都必须执行改任务。

同时过期时间的大小还代表着任务的优先级。
任务在执行过程中顺便收集了每个 FiberNode 的副作用，将有副作用的节点通过 firstEffect、lastEffect、nextEffect 形成一条副作用单链表 AI(TEXT)-B1(TEXT)-C1(TEXT)-C1-C2(TEXT)-C2-B1-B2(TEXT)-B2-A。

其实最终都是为了收集到这条副作用链表，有了它，在接下来的渲染阶段就通过遍历副作用链完成 DOM 更新。这里需要注意，更新真实 DOM 的这个动作是一气呵成的，不能中断，不然会造成视觉上的不连贯。
关于 React Fiber 的思考

1. 能否使用生成器（generator）替代链表
   在 Fiber 机制中，最重要的一点就是需要实现挂起和恢复，从实现角度来说 generator 也可以实现。那么为什么官方没有使用 generator 呢？猜测应该是是性能方面的原因。生成器不仅让您在堆栈的中间让步，还必须把每个函数包装在一个生成器中。一方面增加了许多语法方面的开销，另外还增加了任何现有实现的运行时开销。性能上远没有链表的方式好，而且链表不需要考虑浏览器兼容性。
2. Vue 是否会采用 Fiber 机制来优化复杂页面的更新
   这个问题其实有点搞事情，如果 Vue 真这么做了是不是就是变相承认 Vue 是在”集成” Angular 和 React 的优点呢？React 有 Fiber，Vue 就一定要有？
   两者虽然都依赖 DOM Diff，但是实现上且有区别，DOM Diff 的目的都是收集副作用。Vue 通过 Watcher 实现了依赖收集，本身就是一种很好的优化。所以 Vue 没有采用 Fiber 机制，也无伤大雅。
   总结
   React Fiber 的出现相当于是在更新过程中引进了一个中场指挥官，负责掌控更新过程，足球世界里管这叫前腰。抛开带来的性能和效率提升外，这种“化整为零”和任务编排的思想，可以应用到我们平时的架构设计中。

作者：政采云前端团队
链接：https://juejin.cn/post/6911681589558640654
来源：掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

(转载) 如何利用 JavaScript 实现并发控制

原文地址: https://juejin.cn/post/6912220538286899207?utm_source=gold_browser_extension#heading-4
引申出的FixedArray、HashTable值得大家了解下

一、前言

  在开发过程中，有时会遇到需要控制任务并发执行数量的需求。

  例如一个爬虫程序，可以通过限制其并发任务数量来降低请求频率，从而避免由于请求过于频繁被封禁问题的发生。

  接下来，本文介绍如何实现一个并发控制器。

二、示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

const task = timeout => new Promise((resolve) => setTimeout(() => {
    resolve(timeout);
}, timeout))

const taskList = [1000, 3000, 200, 1300, 800, 2000];

async function startNoConcurrentControl() {
    console.time(NO_CONCURRENT_CONTROL_LOG);
    await Promise.all(taskList.map(item => task(item)));
    console.timeEnd(NO_CONCURRENT_CONTROL_LOG);
}

startNoConcurrentControl();

  上述示例代码利用 Promise.all 方法模拟6个任务并发执行的场景，执行完所有任务的总耗时为 3000 毫秒。

  下面会采用该示例来验证实现方法的正确性。

三、实现

  由于任务并发执行的数量是有限的，那么就需要一种数据结构来管理不断产生的任务。

  队列的「先进先出」特性可以保证任务并发执行的顺序，在 JavaScript 中可以通过「数组来模拟队列」：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

class Queue {
    constructor() {
        this._queue = [];
    }

    push(value) {
        return this._queue.push(value);
    }

    shift() {
        return this._queue.shift();
    }

    isEmpty() {
        return this._queue.length === 0;
    }
}

    对于每一个任务，需要管理其执行函数和参数：

class DelayedTask {
    constructor(resolve, fn, args) {
        this.resolve = resolve;
        this.fn = fn;
        this.args = args;
    }
}

    接下来实现核心的 TaskPool 类，该类主要用来控制任务的执行：

class TaskPool {
    constructor(size) {
        this.size = size;
        this.queue = new Queue();
    }

    addTask(fn, args) {
        return new Promise((resolve) => {
            this.queue.push(new DelayedTask(resolve, fn, args));
            if (this.size) {
                this.size--;
                const { resolve: taskResole, fn, args } = this.queue.shift();
                taskResole(this.runTask(fn, args));
            }
        })
    }

    pullTask() {
        if (this.queue.isEmpty()) {
            return;
        }

        if (this.size === 0) {
            return;
        }

        this.size++;
        const { resolve, fn, args } = this.queue.shift();
        resolve(this.runTask(fn, args));
    }

    runTask(fn, args) {
        const result = Promise.resolve(fn(...args));

        result.then(() => {
            this.size--;
            this.pullTask();
        }).catch(() => {
            this.size--;
            this.pullTask();
        })

        return result;
    }
}

  TaskPool 包含三个关键方法：

• addTask: 将新的任务放入队列当中，并触发任务池状态检测，如果当前任务池非满载状态，则从队列中取出任务放入任务池中执行。
• runTask: 执行当前任务，任务执行完成之后，更新任务池状态，此时触发主动拉取新任务的机制。
• pullTask: 如果当前队列不为空，且任务池不满载，则主动取出队列中的任务执行。

接下来，将前面示例的并发数控制为2个：

1
2
3
4
5
6
7
8
9

const cc = new ConcurrentControl(2);

async function startConcurrentControl() {
    console.time(CONCURRENT_CONTROL_LOG);
    await Promise.all(taskList.map(item => cc.addTask(task, [item])))
    console.timeEnd(CONCURRENT_CONTROL_LOG);
}

startConcurrentControl();

执行流程如下：

最终执行任务的总耗时为 5000 毫秒。

四、高阶函数优化参数传递

1
2

await Promise.all(taskList.map(item => cc.addTask(task, [item])))

  手动传递每个任务的参数的方式显得非常繁琐，这里可以通过「高阶函数实现参数的自动透传」：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

addTask(fn) {
    return (...args) => {
        return new Promise((resolve) => {
            this.queue.push(new DelayedTask(resolve, fn, args));

            if (this.size) {
                this.size--;
                const { resolve: taskResole, fn: taskFn, args: taskArgs } = this.queue.shift();
                taskResole(this.runTask(taskFn, taskArgs));
            }
        })
    }
}

  改造之后的代码显得简洁了很多：

await Promise.all(taskList.map(cc.addTask(task)))

五、优化出队操作
  数组一般都是基于一块「连续内存」来存储，当调用数组的 shift 方法时，首先是删除头部元素（时间复杂度 O(1)），然后需要将未删除元素左移一位（时间复杂度 O(n)），所以 shift 操作的时间复杂度为 O(n)。

  由于 JavaScript 语言的特性，V8 在实现 JSArray 的时候给出了一种空间和时间权衡的解决方案，在不同的场景下，JSArray 会在 FixedArray 和 HashTable 两种模式间切换。

  在 hashTable 模式下，shift 操作省去了左移的时间复杂度，其时间复杂度可以降低为 O(1)，即使如此，shift 仍然是一个耗时的操作。

  在数组元素比较多且需要频繁执行 shift 操作的场景下，可以通过 「reverse + pop」 的方式优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

const Benchmark = require('benchmark');
const suite = new Benchmark.Suite;

suite.add('shift', function() {
    let count = 10;
    const arr = generateArray(count);
    while (count--) {
        arr.shift();
    }
})
.add('reverse + pop', function() {
    let count = 10;
    const arr = generateArray(count);
    arr.reverse();
    while (count--) {
        arr.pop();
    }
})
.on('cycle', function(event) {
    console.log(String(event.target));
})
.on('complete', function() {
    console.log('Fastest is ' + this.filter('fastest').map('name'));
    console.log('\n')
})
.run({
    async: true
})

  通过 benchmark.js 跑出的基准测试数据，可以很容易地看出哪种方式的效率更高：

  回顾之前 Queue 类的实现，由于只有一个数组来存储任务，直接使用 reverse + pop 的方式，必然会影响任务执行的次序。

  这里就需要引入双数组的设计，一个数组负责入队操作，一个数组负责出队操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class HighPerformanceQueue {
    constructor() {
        this.q1 = []; // 用于 push 数据
        this.q2 = []; // 用于 shift 数据
    }

    push(value) {
        return this.q1.push(value);
    }

    shift() {
        let q2 = this.q2;
        if (q2.length === 0) {
            const q1 = this.q1;
            if (q1.length === 0) {
                return;
            }
            q2 = this.q2 = q1.reverse();
        }

        return q2.pop();
    }

    isEmpty() {
        if (this.q1.length === 0 && this.q2.length === 0) {
            return true;
        }
        return false;
    }
}

最后通过基准测试来验证优化的效果：

作者：descire
链接：https://juejin.cn/post/6912220538286899207
来源：掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

算法时间与空间复杂度

算法、数据结构在我们的日常工作中还是很常见的，只要你细心观察，就会发现算可以体现在我们工作中的各个层面.
例如:

• 浏览器的历史中的前进后退是不是可以把它看做一个线性的栈结构，history的pop、push对应这个栈的出栈、压栈.
• const obj = {}; let obj2 = {}; let a = 1; const a = 1; 用数据结构的思维也可以更好的理解ES6的特性。

随着计算机行业发展，不管是前端亦或是后端，算法都是进阶的一个绊脚石，可以说不会算法永远也成不了一个合格
的高级工程师，想要进大厂确实要会些算法，但是它并不只是为了面试，它和我们的程序是息息相关的.

什么是数据结构

数据结构其实就是是程序存储组织数据的方式，一个数据结构是由程序中的数据元素按照某种逻辑关系组织起来的，是若干个数据元素的组合.

数据结构是程序中处理数据的基本单位，在程序中作为一个整体来使用

例如一个数字 1 或者一个字符 A，它是一种数据结构

例如一个数组 [‘dog’, ‘cat’, ‘wolves’]，它是由字符串组合而成的数组，也是一种数据结构

通俗来说，用一定格式组成的数据都是数据结构，我们比较常见的数据结构有字符串、数组、对象、堆、栈、链表、树、哈希表等等，你可能对着其中的一些数据结构并不了解，不要担心，你并不需要立刻知道它们都是什么，对于前端来说，我们使用 JavaScript 这个令我们又爱又恨的语言，它本身就存在的数据结构很少，那么对于像链表、树等等这些结构都是通过对象来模拟的，这点要先知道.

在许多程序设计当中，数据结构的选择是一个基本的设计考虑因素，系统实现的困难程度和系统构造的质量都严重依赖于是否选择了最优的数据结构，选择最优的数据结构能够有效的提高运行的效率和节约存储空间的使用，但是要知道，没有十全十美的数据结构，每种数据结构都有局限性同样也有优点，要根据需求来选择合适的数据结构.

什么是算法

什么是算法，我们都知道 1+2+3=6，为什么等于 6 呢，你可能会说，1 加 2等于 3，两个 3 相加等于 6，这是小学生都会的数学常识，它就是广义上的算法

算法其实就是解决一个问题的完整步骤描述，是指完成一个任务准确而完整的步骤描述

算法的设计很多时候需要取决于数据结构，而算法的实现更依赖于采用的数据结构

提出一个问题的算法是一个从抽象到具体的过程

分析问题，选择数据结构，得出初步的解决方法

将解决方法合理地拆分，整理成许多步骤

为重复的步骤选择合理的循环变量

使用易转化为程序实现的自然语言简练地描述算法

了解了什么是算法之后，我们来看时间和空间复杂度，衡量不同算法之间的优劣我们通常从两个维度来考究

• 时间维度：指执行代码所消耗的时间，即时间复杂度
• 空间维度：指执行代码所消耗的空间，即空间复杂度

接下来就开始逐步剖析时间和空间复杂度了，先说时间复杂度

时间复杂度

在说时间复杂度之前，我们首先要理解一个概念即代码执行次数，也可称之为语句频度或时间频度，用 T(n) 表示

我们用例子来一步一步阐述，首先我们来看函数 fn1

1
2
3
4
5

function fn1(){
    console.log("run")
    console.log("end")
}

我们来看这个函数中的语句会执行多少次

很明显此函数内部只有两个语句，即 console.log(“run”) 和 console.log(“end”)，那么我们说这个函数体内代码执行次数是 2

我们再来看函数 fn2

1
2
3
4
5
6

function fn2(n){
    for(let i = 0; i < n; i++){
        console.log("run")
    }
}

我们先来看函数 fn2 中有几条可执行语句

1
2
3
4
5

let i = 0
i < n
i++
console.log("run")

我们假设 n = 3，然后依次带入进去，看看各个执行语句执行了多少次
let i = 0 此条声明语句只在第一次 for 循环声明时执行 1 次
i < n 此条语句执行次数根据形参 n 的大小变化，n = 3 时，即 i=0,i=1,i=2,i=3 时会执行，即此条语句执行次数为 n + 1 次
i++ 此条语句执行次数也是根据形参 n 的大小变化，n = 3 时，即 i=0,i=1,i=2 时会执行，即 n 次
console.log(“run”) 此条语句执行次数还是根据形参 n 的大小变化，n = 3 会执行 3 次，那么此语句在函数内部即会执行 n 次

1 + (n + 1) + n + n = (3n + 2)

那么函数 fn2 内共执行 3n + 2 次

一段代码的总执行次数我们通常会用 T(n) 来表示，那么调用一次上面 fn1/fn2 两函数的总执行次数即

T(n) = 2 // fn1
T(n) = 3n + 2 // fn2

上面的 n，指的是为问题的规模，即输入数据的大小或者说数量，你也可以简单的理解为 T 就是函数本身，n 就是参数，也就是说

函数 fn1 任何情况下执行次数都为 2

函数 fn2 的总执行次数会根据 n 的大小变化而产生一个变化

我们思考一下，我们可以使用一段代码的执行总次数来衡量执行速度吗？

答案当然是不行的，当代码行数比较多的时候，我们一条一条的数来计算执行总次数太麻烦了，例如函数中套用函数时、循环中套用循环时，想要精确计算执行次数都是非常麻烦的

所以，在算法中，我们一般用 T(n) 简化后的估算值来表达代码执行的速度，通常我们用大些字母 O 来表示，即大 O 表示法，由于是估算，它表示的是代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度

明确了这个概念以后，我们就可以来算时间复杂度了，还是用上面 fn1/fn2 两函数例

// fn1
T(n) = 2

// fn2
T(n) = 3n + 2

首先我们来看函数 fn1，它的执行总次数为 2，一个 常数(常数级)，也就是说此函数无论何时它的总执行次数都是 2，是一个不变的值，那么我们使用时间复杂度 O 来表示时直接估算为 1 就可以，即时间复杂度为 O(1)

我们再来看函数 fn2 ，它的执行次数 T(n) 是 3n + 2 即 常数n + 常数，这里我们完全可以看成 常数n 和 +常数 两部分，随着 n 的增大，只有前一个部分会有变化，后面是不变的，所以在表示时间复杂度时就可以忽略后面不变的常数，即 常数n，而 常数n 中过的常数我们也可以直接当做 1，或者说忽略掉这个作为系数的常数，那么最终可以得出函数 fn2 的时间复杂度为 n，即 O(n)

PS：晓得可能有人把数学知识还给老师了，所以解释下

常数： 常数就是指平常的数值，可简单的理解为固定不变的数值

系数： 系数指代数式的单项式中的数字因数，例如 a = 1a则它的系数为1,2b=2b ，则它的系数为 2

我们再来举个例子，如下面这个多项式代指一个函数的 T(n)，求它的时间复杂度

T(n) = 10n^4 + 100n^2 + 1000

其实，对于多项式，我们只需要保留最高次项就行了，也就说，保留 n 的最高次方数就可以了，这个例子中保留的也就是 n 的 4 次方，系数和常数皆可以忽略，最终得到的时间复杂度即为 O(n^4)

结论：

T(n) 为常数时，时间复杂度为 O(1) ，反之时间复杂度为 O(保留T(n)的最高次项并去掉最高次项的系数)

接下来，我们看几个例子来判断下几段代码的时间复杂度

例1：

1
2
3
4
5
6
7
8

function fn01(){
    console.log("你看这是啥")
    console.log("这是一个输出")
    console.log("哈哈哈")
    let a = 1
    return a
}

上面这个函数 fn01 中只有一条条的语句，共执行 5 次，毫无变化，时间复杂度即 O(1) ，此为常数级时间复杂度

例2：

1
2
3
4
5
6

function fn02(n){
    for(let i = 0; i < n; i++){
        console.log("这是一个输出🎓")
    }
}

如上，函数 fn02 同上文中的例子 fn2，一个循环，时间复杂度即为 O(n) ，此为线性级时间复杂度

例3：

1
2
3
4
5
6
7
8
9

function fn03(n){
    for(let i = 0; i < n; i++){
        console.log("外层循环")
        for(let j = 0; j < n; j++){
        console.log("内层循环")
        }
    }
}

这个题和上面就不太一样了，我们先单独看内部的循环，内部循环大概会执行 n 次，再来看外部循环又会执行 n 次，最终也就是 n * n = n^2，即函数 fn03 的时间复杂度为 O(n^2) ，此为平方级时间复杂度，如果是三层循环也就是时间复杂度为 O(n^3) 时，即立方级时间复杂度

从这里我们就可以看出来，一段代码有多少层循环，时间复杂度就是 n 的多少次方，所以尽量避免多层循环嵌套

例4：

我们再来看下面这个函数 fn04

1
2
3
4
5
6
7
8
9
10
11
12
13

function fn04(n){
    for(let i = 0; i < n; i++){
        console.log("外层循环")
        for(let j = 0; j < n; j++){
        console.log("内层循环")
        }
    }
    
    for(let i = 0; i < n; i++){
        console.log("哈哈哈")
    }
}

此函数中有一个双循环，有一个单循环，即执行次数大概是 n^2 + n，根据我们上面说的保留最高次项，那么函数 fn04 的时间复杂度即为 O(n^2)

例5：

算法中肯定不只是上面那种寻常的循环，再来看下面这一个

1
2
3
4
5
6
7
8
9

function fn05(n){
    for(let i = 0; i < n; i++){
        console.log("外层循环")
        for(let j = i; j < n; j++){
        console.log("内层循环")
        }
    }
}

其实遇到这种，我们直接带入进去试一试即可知其规律

当 i = 0 时，里层循环会执行 n 次

当 i = 1 时，里层循环会执行 n - 1 次

当 i = 2 时，里层循环会执行 n - 2 次

当 i = 3 时，里层循环会执行 n - 3 次

这个时候我们就发现了规律，每当 i 增加 1，里层循环就少执行 1 次，那么就简单了

当 i = n - 2 时，里层循环会执行 2 次

当 i = n - 1 时，里层循环会执行 1 次

最终我们把 n 个里层循环的执行次数相加即可得出最终的一个不精确的总执行次数

T(n) = n + (n - 1) + (n - 2) + … + 3 + 2 + 1

如上，这是一个等差数列，嗯，晓得，会补充

如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，而这个常数叫做等差数列的公差，公差常用字母 d 表示

例如：1,3,5,7,9……（2n-1) ，等差数列 S(n) 的通项公式为：S(n) = S1 + (n-1) * d，前 n 项和公式如下

S(n) = nS1 + n(n - 1)*d/2

// 或

S(n) = n*(S1 + Sn)/2

如此我们计算结果就成，我们上面的数列中，公差 d 为 -1，带入公式即可，第二个公式简单，用第二个好了，计算结果都是一样的

// n*(S1 + Sn)/2

n*(n + 1)/2 = (n^2 + n)/2 = (1/2)n^2 + (1/2)n

最终我们得到了 (1/2)n^2 + (1/2)n ，按照上文中取最高次项去掉系数，即时间复杂度为 O(n^2)

例6：

再来看一个例子

1
2
3
4
5
6

function fn06(n){
    for(let i = 1; i < n; i *= 2){
        console.log("run")
    }
}

还是老样子，如果你不晓得怎么看，可以先带入几个参数试一下，看一看规律

我们可以分别使用 n=2, n=4, n=8, n=16，观察其循环中打印次数，当然你也可以直接运行一下代码，过程不过多阐述了，我们直接看结果

n=2 时打印1次 T(n)=1
n=4 时打印2次 T(n)=2
n=8 时打印3次 T(n)=3
n=16 时打印4次 T(n)=4

对于执行次数产生主要影像的就是循环语句中的 i*=2，每次循环 i 都会变成自身的两倍，仔细观察我们就可以得出这样一个规律性结果

n=2 时打印1次 T(n)=1 // 2^1 = 2
n=4 时打印2次 T(n)=2 // 2^2 = 4
n=8 时打印3次 T(n)=3 // 2^3 = 8
n=16 时打印4次 T(n)=4 // 2^4 = 16

根据上面的规律我们不难发现，那么2^执行次数=n，即 2^T(n)=n ，我们求 T(n)，调个就行了，也就是以 2 为底 n 的对数，即 T(n)=log_2 n

PS：又来补数学了

对数： 假如 a^n=b，即 a 的 n 次方等于 b，我们求 n 的值，那么这里为了方便表示就可以写成 log_a b，即以 a 为底 b 的对数，a 是底数，b 是真数，而 n 就是对数

你可能会在纠结为什么只观察循环中的打印次数而不计算其所有的执行次数，原因上面也说过了，这些固有的常数及系数完全可以忽略，好吧，我们再最后推一遍

中间输出为 log_2 n 次，let i = 1 只会执行一次，i<n 会执行 log_2 n + 1 次，i*=2 也会执行 log_2 n 次，加起来就是 log_2 n + log_2 n + 1 + log_2 n，即 3log_2 n + 2，除去系数 3 和常数 2，我们得出了 log_2 n ，在时间复杂度的计算中 log 的底数也是可以省略的，所以最终函数 fn06 的时间复杂度为 O(log n) ，也就是对数级时间复杂度

例7：

最后在给大家来一个例子吧

1
2
3
4
5
6
7
8
9

function fn07(n,m){
    for(let i = 0; i < n; i++){
        while(j < m){
        console.log("你看懂了吗")
        j = j * 2
        }
    }
}

如上图，此函数有两个参数，对应了里外两个循环，我们先从内部循环看起，眼熟吗？其实内部循环和上题函数 fn06 中的循环是一样的，只是一个用的 for ，一个用的 while，上题中的时间复杂度我们就不再叙述了，那么内层循环时间复杂度为 O(log n)

我们再来看外层循环，也是上面解释过的，单看外层循环时间复杂度是 O(n)

两个循环是嵌套关系，相乘就可以了，所以函数 fn07 的时间复杂度即为 O(n*log n) ，也就是线性对数级时间复杂度

正如此函数输出，你看懂了吗？

常见的时间复杂度量级有

常数级 O(1)
对数级 O(log n)
线性级 O(n)
线性对数级 O(n*log n)
平方级 O(n^2)
立方级 O(n^3)
K次方级 O(n^k)
指数级 O(2^n)
上面从上到下依次时间复杂度越来越大，执行效率越来越低，大部分常用的在上面的图表中都有展示

所以在程序或是刷题中，我们应该尽量使用低时间复杂度的方法

时间复杂度就到此为止了，我们也列举了常见的时间复杂度，接下来我们来看看空间复杂度

空间复杂度

空间复杂度其实就是对一个算法或者说一段代码在运行过程中占用存储空间大小表达方式

我们上面讲过了时间复杂度，那么再来说空间复杂度会简单的很多

空间复杂度也就是 S(n) ，它同样会用大O表示法来表示，我们直接上例子

例1：

1
2
3
4
5
6

function fn001(n){
    for(let i = 0; i < n; i++){
        console.log("空间复杂度")
    }
}

首先，我们知道，空间复杂度和存储空间有关，而存储空间是由什么决定的，肯定是声明的变量啊，我们直接来找函数 fn001 中的变量声明，只有一个 i ，也就是说此函数只有开辟了一块空间供 i 使用，那么空间复杂度 S(n) 即为 O(1) ，你可能会说 i 不是一直在变吗，是的它是在变，但是不管怎么变，它还是一个数字，占用空间大小都一致

空间复杂度和时间复杂度一样，当代码里声明的变量是一个常量，不会根据传入值的变化而变化，那么也它的空间复杂度是 O(1)

例2：

1
2
3
4
5
6
7

function fn002(n){
    let arr = []
    while(n--){
        arr.push(n)
    }
}

这个例子中我们声明了一个数组，我们知道数组中是可以存各种类型的，在循环中，我们根据 n 的大小向数组 arr 中 push 元素，所以，n 多大，数组就有多少元素，就占用了多少空间，所以空间复杂度S(n) = O(n)

空间复杂度小结

空间复杂度里，只列出了两个例子，是因为一般情况下，我们用不到其他的，空间复杂度一般只会是 O(1)/O(n)/O(n^2)，其它的很少见，当然也有，我们在知道了时间复杂度再分析空间复杂度也很好分析，就不过多赘述了

关于分析空间复杂度，其实我们直接从声明的变量入手就可以，看函数体内声明的变量根据传入值的变化而变化来分析

另外，这里我们没有列举递归情况，请注意，递归就是函数套函数，像俄罗斯套娃一样的，这中间其实有一个问题，我们知道，递归函数，每层递归里都会开辟一个递归栈，每次递归产生的变量等空间消耗都会存在递归栈中，这也是一个空间，不管你有没有声明变量，只要递归了递归栈它都存在，也就是说只要存在递归的情况，基本上最少的空间复杂度也是 O(n) 了，所以我们尽可能的在能使用迭代的情况下就不使用递归

时间 VS 空间

开头我们说了，评价一个算法的效率我们主要是从它的时间和空间两个维度看，但是，通常我们在算法中，时间和空间就是鱼和熊掌的关系，这时候可能一道算法题有两种解法，一种时间复杂度低，但空间复杂度稍高，另一种则反之

这个时候怎么办呢？细品就知道了，在开发中，我们一般都是时间优于空间的，你想啊，一个程序，用户不会关心的占用了多少内存，但是他会关心你这个程序他在使用时的执行速度，况且，空间也就是磁盘，现阶段磁盘我们可以花钱扩容，时间上就没这么简单了，所以某些相对的情况下，空间换时间是可以令人接受的

虽说空间换时间可行，但也不能一味的空间换时间，我们还是要尽可能降低两个维度的复杂度，少数对立情况下，可空间换时间

我们在刷算法的时候，不是刷完了就完事了，我们还要去分析我们的题解对应的时间及空间复杂度，可以分析多种题解之间的复杂度，对比找出最优解

参考文章

https://zhuanlan.zhihu.com/p/50479555

examples

1
2
3

git commit -m "feat: :sparkles: built a Tank, yesterday."

git commit -m "feat: :sparkles: built a Rocket, today."

Git提交添加emoji图标

https://gitmoji.carloscuesta.me/

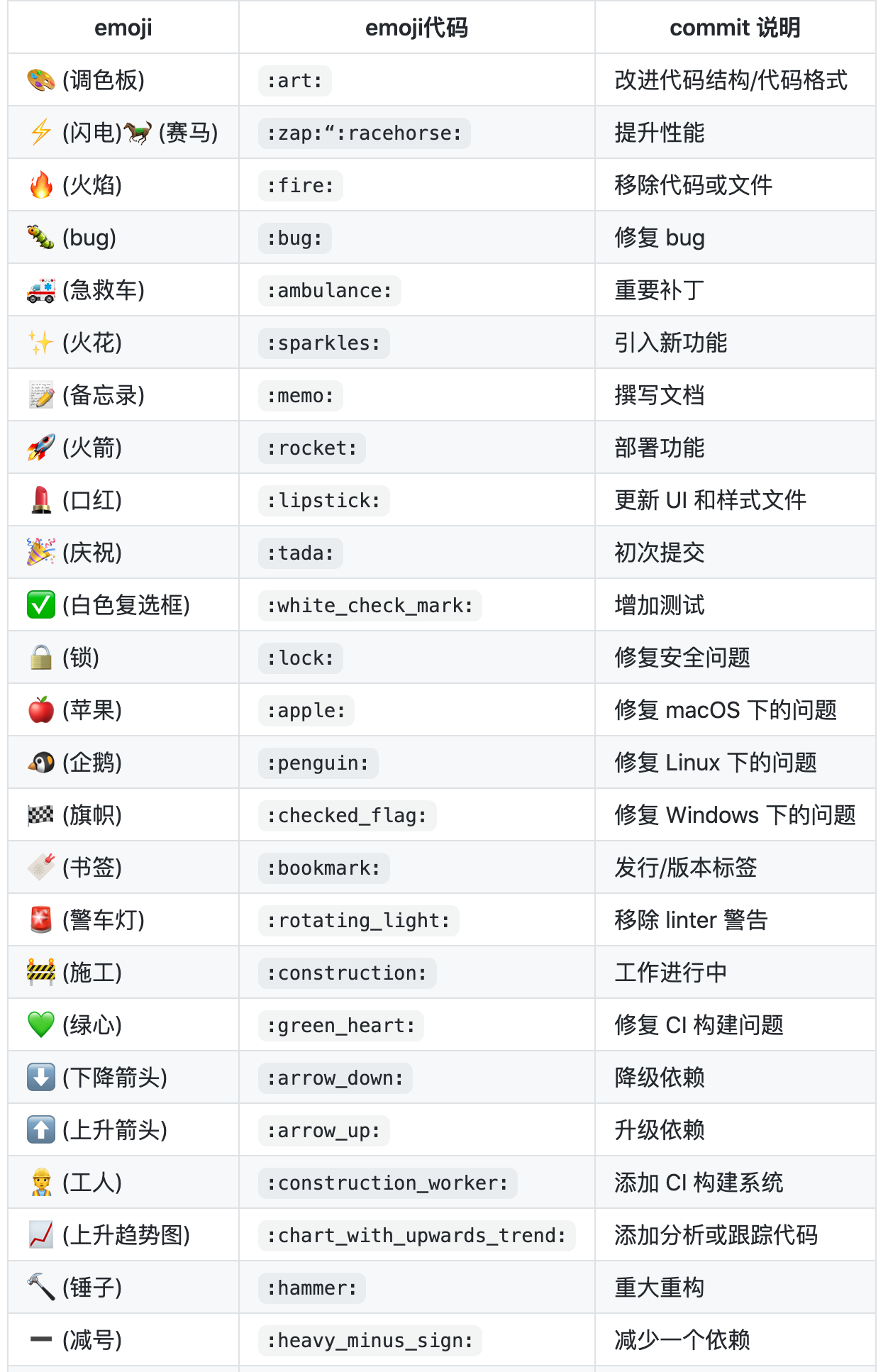
在提交内容的前面增加了emoji标签： **:emoji:**，其中emoji是表情图标的标签，列表见下面的附录表格。